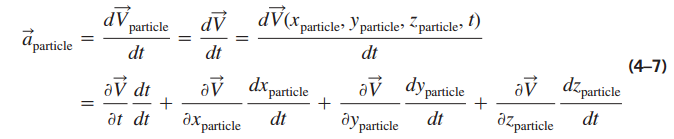Mekanika adalah ilmu fisika tertua yang mempelajari benda diam dan bergerak di bawah pengaruh gaya. Cabang ilmu mekanika yang mempelajari benda diam disebut statika, sedangkan cabang yang mempelajari benda bergerak disebut dinamika. Subkategori mekanika fluida didefinisikan sebagai ilmu yang mempelajari perilaku fluida dalam keadaan diam (statis fluida) atau dalam gerak (dinamika fluida), dan interaksi fluida dengan padatan atau fluida lain pada batasnya. Mekanika fluida juga disebut sebagai dinamika fluida dengan mempertimbangkan fluida diam sebagai kasus gerak khusus dengan kecepatan nol (Gbr. 1–1).

Mekanika fluida mempelajari tentang zat cair dan gas yang bergerak atau diam.
Sumber D.Falconer PhotoLink Getty RF

Mekanika fluida sendiri juga terbagi menjadi beberapa kategori.

Ilmu yang mempelajari tentang gerak fluida yang dapat diperkirakan sebagai fluida yang tidak dapat dimampatkan (seperti zat cair, terutama air, dan gas dengan kecepatan rendah) biasanya disebut dengan hidrodinamika.

Subkategori hidrodinamika adalah hidrolika, yang mempelajari aliran cairan dalam pipa dan saluran terbuka.

Dinamika gas berkaitan dengan aliran fluida yang mengalami perubahan densitas yang signifikan, seperti aliran gas melalui nozel dengan kecepatan tinggi.

Kategori aerodinamika berkaitan dengan aliran gas (terutama udara) di atas benda seperti pesawat terbang, roket, dan mobil dengan kecepatan tinggi atau rendah.

Beberapa kategori khusus lainnya seperti meteorologi, oseanografi, dan hidrologi berhubungan dengan aliran yang terjadi secara alami.

Dalam Sub Bab Ini ada 2 Bahasan Yaitu

1-1-1. Apa Itu Cairan?

1-1-2. Area Penerapan Mekanika Fluida

Apa Itu Cairan ?

Anda akan ingat dari ilmu fisika bahwa suatu zat ada dalam tiga fase utama: padat, cair, dan gas. (Pada suhu yang sangat tinggi, ia juga ada sebagai plasma.) Zat dalam fase cair atau gas disebut fluida. Perbedaan antara benda padat dan zat cair didasarkan pada kemampuan zat tersebut untuk menahan tegangan geser (atau tangensial) yang cenderung mengubah bentuknya. Benda padat dapat menahan tegangan geser yang diberikan dengan cara melakukan deformasi, sedangkan zat cair akan terus menerus mengalami deformasi karena pengaruh tegangan geser, tidak peduli seberapa kecilnya. Pada benda padat, tegangan sebanding dengan regangan, tetapi pada zat cair, tegangan sebanding dengan laju regangan. Ketika gaya geser konstan diterapkan, padatan akhirnya berhenti berubah bentuk pada sudut regangan tetap, sedangkan fluida tidak pernah berhenti berubah bentuk dan mendekati laju regangan yang konstan.

Bayangkan sebuah balok karet persegi panjang yang ditempatkan rapat di antara dua pelat. Saat pelat atas ditarik dengan gaya F sementara pelat bawah ditahan, balok karet berubah bentuk, seperti ditunjukkan pada Gambar 1–2.

Deformasi balok karet yang ditempatkan di antara dua pelat sejajar di bawah pengaruh gaya geser. Tegangan geser yang ditunjukkan adalah pada karet—tegangan geser yang sama besar namun berlawanan arah bekerja pada pelat atas.

Sudut deformasi a (disebut regangan geser atau perpindahan sudut) meningkat sebanding dengan gaya yang diterapkan F. Dengan asumsi tidak ada slip antara karet dan pelat, permukaan atas karet mengalami perpindahan sebesar yang sama dengan perpindahan pelat atas sedangkan permukaan bawah tetap diam. Dalam kesetimbangan, gaya total yang bekerja pada pelat atas dalam arah horizontal harus sama dengan nol, sehingga gaya yang sama besar dan berlawanan dengan F harus bekerja pada pelat. Gaya berlawanan yang timbul pada antarmuka pelat-karet akibat gesekan dinyatakan sebagai F = tA, dengan t adalah tegangan geser dan A adalah bidang kontak antara pelat atas dan karet. Ketika gaya dihilangkan, karet kembali ke posisi semula. Fenomena ini juga dapat diamati pada benda padat lain seperti balok baja asalkan gaya yang diterapkan tidak melebihi rentang elastis. Jika percobaan ini diulangi dengan suatu fluida (misalnya dengan dua pelat besar sejajar yang ditempatkan dalam suatu perairan besar), lapisan fluida yang bersentuhan dengan pelat atas akan bergerak bersama pelat secara terus menerus dengan kecepatan pelat berapa pun kecepatannya. kecil gaya F. Kecepatan fluida akan berkurang seiring bertambahnya kedalaman karena gesekan antar lapisan fluida, mencapai nol di pelat bawah.

Anda ingat dari ilmu statika bahwa tegangan didefinisikan sebagai gaya per satuan luas dan ditentukan dengan membagi gaya dengan luas tempat gaya bekerja. Komponen normal gaya yang bekerja pada permukaan per satuan luas disebut tegangan normal, dan komponen tangensial gaya yang bekerja pada permukaan per satuan luas disebut tegangan geser (Gbr. 1–3).

Tegangan normal dan tegangan geser pada permukaan elemen fluida. Untuk fluida yang diam, tegangan gesernya adalah nol dan tekanan merupakan satu-satunya tegangan normal.

Dalam fluida yang diam, tegangan normalnya disebut tekanan. Fluida yang diam berada pada keadaan tegangan geser nol. Ketika dinding dilepas atau wadah cairan dimiringkan, terjadi pergeseran saat cairan bergerak untuk membentuk kembali permukaan bebas horizontal.

Dalam cairan, kelompok molekul dapat bergerak relatif satu sama lain, namun volumenya relatif konstan karena kuatnya gaya kohesif antar molekul. Akibatnya, zat cair mengambil bentuk wadahnya, dan membentuk permukaan bebas dalam wadah yang lebih besar di bawah pengaruh medan gravitasi. Sebaliknya, gas memuai hingga memenuhi dinding wadah dan memenuhi seluruh ruang yang tersedia. Hal ini karena jarak molekul-molekul gas sangat jauh, dan gaya kohesif di antara keduanya sangat kecil. Berbeda dengan cairan, gas dalam wadah terbuka tidak dapat membentuk permukaan bebas (Gbr. 1–4).

Berbeda dengan cairan, gas tidak membentuk permukaan bebas, dan ia mengembang memenuhi seluruh ruang yang tersedia.

Meskipun pada banyak kasus benda padat dan cairan mudah dibedakan, perbedaan ini tidak begitu jelas pada beberapa kasus yang berada pada batas tertentu. Misalnya, aspal tampak dan berperilaku padat karena tahan terhadap tegangan geser dalam waktu singkat. Namun, ketika gaya-gaya ini diberikan dalam jangka waktu yang lama, aspal akan mengalami deformasi secara perlahan dan berperilaku seperti fluida. Beberapa campuran plastik, timbal, dan bubur menunjukkan perilaku serupa. Kasus-kasus yang berada di ambang batas tersebut berada di luar cakupan teks ini. Fluida yang kita bahas dalam teks ini akan dikenali dengan jelas sebagai fluida.

Ikatan antarmolekul paling kuat pada benda padat dan paling lemah pada gas. Salah satu alasannya adalah molekul-molekul dalam padatan tersusun rapat, sedangkan dalam gas mereka terpisah dalam jarak yang relatif jauh (Gbr. 1–5).

Susunan atom-atom dalam berbagai fase: (a) molekul-molekul berada pada posisi yang relatif tetap dalam zat padat, (b) kelompok-kelompok molekul bergerak satu sama lain dalam fase cair, dan (c) masing-masing molekul bergerak secara acak dalam fase gas.

Molekul-molekul dalam padatan tersusun dalam pola yang berulang-ulang. Karena kecilnya jarak antara molekul-molekul dalam zat padat, gaya tarik-menarik molekul satu sama lain menjadi besar dan menjaga molekul-molekul pada posisi tetap. Jarak molekul dalam fase cair tidak jauh berbeda dengan fase padat, hanya saja molekul-molekulnya tidak lagi berada pada posisi tetap relatif satu sama lain dan mereka dapat berputar dan berpindah dengan bebas. Dalam cairan, gaya antarmolekul lebih lemah dibandingkan padatan, namun masih kuat dibandingkan dengan gas. Jarak antar molekul umumnya bertambah sedikit ketika benda padat berubah menjadi cair, kecuali air.

Dalam fase gas, molekul-molekulnya berjauhan satu sama lain, dan susunan molekul tidak ada. Molekul-molekul gas bergerak secara acak, terus-menerus bertabrakan satu sama lain dan dengan dinding wadah tempat mereka terkurung. Khususnya pada kepadatan rendah, gaya antarmolekul sangat kecil, dan tumbukan adalah satu-satunya cara interaksi antar molekul. Molekul dalam fase gas mempunyai tingkat energi yang jauh lebih tinggi dibandingkan dalam fase cair atau padat. Oleh karena itu, gas harus melepaskan sejumlah besar energinya sebelum dapat mengembun atau membeku. Gas dan uap sering digunakan sebagai kata sinonim. Fasa uap suatu zat biasa disebut gas bila berada di atas suhu kritis. Uap biasanya menyiratkan bahwa fase saat ini tidak jauh dari keadaan kondensasi.

Setiap sistem fluida praktis terdiri dari sejumlah besar molekul, dan sifat-sifat sistem secara alami bergantung pada perilaku molekul-molekul tersebut. Misalnya, tekanan gas dalam suatu wadah merupakan hasil perpindahan momentum antara molekul dan dinding wadah. Namun, kita tidak perlu mengetahui perilaku molekul gas untuk menentukan tekanan dalam wadah. Cukup dengan memasang pengukur tekanan pada wadah (Gbr. 1–6).

Pendekatan makroskopis atau klasik ini tidak memerlukan pengetahuan tentang perilaku molekul individu dan menyediakan cara langsung dan mudah untuk menganalisis masalah teknik. Pendekatan mikroskopis atau statistik yang lebih rumit, berdasarkan pada perilaku rata-rata kelompok besar molekul individu, agak terlibat dan digunakan dalam teks ini hanya sebagai peran pendukung.

Area Penerapan Mekanika Fluida

Penting untuk mengembangkan pemahaman yang baik tentang prinsip-prinsip dasar mekanika fluida, karena mekanika fluida banyak digunakan baik dalam aktivitas sehari-hari maupun dalam perancangan sistem rekayasa modern mulai dari penyedot debu hingga pesawat supersonik. Misalnya, mekanika fluida memainkan peran penting dalam tubuh manusia. Jantung terus-menerus memompa darah ke seluruh bagian tubuh manusia melalui arteri dan vena, dan paru-paru adalah tempat aliran udara dalam arah bergantian. Semua jantung buatan, mesin pernapasan, dan sistem dialisis dirancang menggunakan dinamika fluida (Gbr. 1–7).

Dinamika fluida digunakan secara luas dalam desain jantung buatan. Yang ditampilkan di sini adalah Jantung Buatan Total Penn State Electric. Foto milik Lab Fotografi Biomedis, Institut Teknik Biomedis Penn State.

Rumah biasa, dalam beberapa hal, adalah ruang pameran yang dipenuhi dengan aplikasi mekanika fluida. Sistem perpipaan untuk air, gas alam, dan limbah untuk setiap rumah dan seluruh kota dirancang terutama berdasarkan mekanika fluida. Hal yang sama juga berlaku untuk jaringan perpipaan dan saluran sistem pemanas dan pendingin udara. Kulkas terdiri dari tabung tempat refrigeran mengalir, kompresor yang memberi tekanan pada refrigeran, dan dua penukar panas tempat refrigeran menyerap dan membuang panas. Mekanika fluida memainkan peran utama dalam desain semua komponen ini. Bahkan pengoperasian kran biasa pun didasarkan pada mekanika fluida.

Kita juga dapat melihat banyak penerapan mekanika fluida pada mobil. Semua komponen yang berkaitan dengan pengangkutan bahan bakar dari tangki bahan bakar ke silinder—saluran bahan bakar, pompa bahan bakar, dan injektor bahan bakar atau karburator—serta pencampuran bahan bakar dan udara di dalam silinder serta pembuangan gas pembakaran di pipa knalpot—dianalisis menggunakan mekanika fluida. Mekanika fluida juga digunakan dalam desain sistem pemanas dan pendingin udara, rem hidrolik, power steering, transmisi otomatis, sistem pelumasan, sistem pendingin blok mesin termasuk radiator dan pompa air, dan bahkan ban. Bentuk mobil model terbaru yang ramping dan ramping adalah hasil dari upaya meminimalkan hambatan dengan menggunakan analisis aliran di permukaan yang ekstensif.

Dalam skala yang lebih luas, mekanika fluida memainkan peran utama dalam desain dan analisis pesawat terbang, kapal, kapal selam, roket, mesin jet, turbin angin, perangkat biomedis, sistem pendingin untuk komponen elektronik, dan sistem transportasi untuk memindahkan air, minyak mentah, dan gas alam. Hal ini juga dipertimbangkan dalam desain bangunan, jembatan, dan bahkan papan reklame untuk memastikan bahwa struktur tersebut dapat menahan beban angin. Berbagai fenomena alam seperti siklus hujan, pola cuaca, naiknya air tanah ke puncak pohon, angin, gelombang laut, dan arus di perairan besar juga diatur oleh prinsip mekanika fluida (Gbr. 1–8) .

Beberapa bidang penerapan mekanika fluida.

SEJARAH SINGKAT MEKANIKA FLUIDA

Salah satu masalah teknis pertama yang dihadapi umat manusia seiring berkembangnya kota adalah penyediaan air untuk keperluan rumah tangga dan irigasi tanaman. Gaya hidup perkotaan kita hanya dapat dipertahankan dengan air yang melimpah, dan jelas dari arkeologi bahwa setiap peradaban prasejarah yang sukses berinvestasi dalam pembangunan dan pemeliharaan sistem air. Saluran air Romawi, beberapa di antaranya masih digunakan, adalah contoh yang paling terkenal. Namun, mungkin rekayasa yang paling mengesankan dari sudut pandang teknis dilakukan di kota Helenistik Pergamon di Turki saat ini. Di sana, dari tahun 283 hingga 133 SM, mereka membangun serangkaian pipa timah dan tanah liat bertekanan (Gbr. 1–9), dengan panjang hingga 45 km yang beroperasi pada tekanan melebihi 1,7 MPa (tinggi 180 m). hampir semua pembangun awal ini hilang dalam sejarah.

Kontribusi paling awal terhadap teori mekanika fluida dibuat oleh matematikawan Yunani Archimedes (285–212 SM). Ia merumuskan dan menerapkan prinsip daya apung dalam uji tak rusak pertama dalam sejarah untuk menentukan kandungan emas pada mahkota Raja Hiero I. Bangsa Romawi membangun saluran air besar dan mendidik banyak orang yang ditaklukkan tentang manfaat air bersih, namun secara keseluruhan mereka memiliki pemahaman yang buruk tentang cairan. teori. (Mungkin mereka seharusnya tidak membunuh Archimedes ketika mereka memecat Syracuse.)

Selama Abad Pertengahan, penerapan mesin fluida perlahan tapi pasti berkembang. Pompa piston yang elegan dikembangkan untuk mengeringkan tambang, dan kincir air serta kincir angin disempurnakan untuk menggiling biji-bijian, menempa logam, dan untuk tugas lainnya. Untuk pertama kalinya dalam sejarah umat manusia, pekerjaan besar dilakukan tanpa kekuatan otot yang dipasok oleh manusia atau hewan, dan penemuan-penemuan ini umumnya dianggap sebagai penyebab terjadinya revolusi industri di kemudian hari. Sekali lagi pencipta sebagian besar kemajuan ini tidak diketahui, namun perangkat itu sendiri telah didokumentasikan dengan baik oleh beberapa penulis teknis seperti Georgius Agricola (Gbr. 1–10).

Renaisans membawa perkembangan berkelanjutan pada sistem dan mesin fluida, namun yang lebih penting, metode ilmiah disempurnakan dan diadopsi di seluruh Eropa. Simon Stevin (1548–1617), Galileo Galilei (1564–1642), Edme Mariotte (1620–1684), dan Evangelista Torricelli (1608–1647) termasuk orang pertama yang menerapkan metode ini pada fluida saat mereka menyelidiki distribusi tekanan hidrostatik dan ruang hampa. . Karya tersebut diintegrasikan dan disempurnakan oleh ahli matematika dan filsuf brilian, Blaise Pascal (1623–1662). Biksu Italia, Benedetto Castelli (1577–1644) adalah orang pertama yang mempublikasikan pernyataan prinsip kontinuitas fluida. Selain merumuskan persamaan gerak benda padat, Sir Isaac Newton (1643–1727) menerapkan hukumnya pada fluida dan mengeksplorasi inersia dan hambatan fluida, pancaran bebas, dan viskositas. Upaya tersebut dikembangkan oleh Daniel Bernoulli (1700–1782), seorang Swiss, dan rekannya Leonard Euler (1707–1783). Bersama-sama, pekerjaan mereka mendefinisikan persamaan energi dan momentum. Risalah klasik Bernoulli tahun 1738, Hydrodynamica, dapat dianggap sebagai teks mekanika fluida pertama. Terakhir, Jean d'Alembert (1717–1789) mengembangkan gagasan tentang komponen kecepatan dan percepatan, ekspresi diferensial dari kontinuitas, dan “paradoks” tentang resistensi nol terhadap gerak seragam tetap pada suatu benda.

Perkembangan teori mekanika fluida hingga akhir abad kedelapan belas berdampak kecil pada bidang teknik karena sifat dan parameter fluida tidak dapat diukur dengan baik, dan sebagian besar teori merupakan abstraksi yang tidak dapat diukur untuk tujuan desain. Hal ini berubah seiring berkembangnya sekolah teknik Perancis yang dipimpin oleh Riche de Prony (1755–1839). Prony (masih dikenal karena remnya untuk mengukur kekuatan poros) dan rekan-rekannya di Paris di École Polytechnique dan École des Ponts et Chaussées adalah orang pertama yang mengintegrasikan kalkulus dan teori ilmiah ke dalam kurikulum teknik, yang menjadi model bagi seluruh Dunia. (Jadi sekarang Anda tahu siapa yang harus disalahkan atas tahun pertama Anda yang menyakitkan.) Antonie Chezy (1718–1798), Louis Navier (1785–1836), Gaspard Coriolis (1792–1843), Henry Darcy (1803–1858), dan banyak lainnya kontributor teknik dan teori fluida adalah siswa dan/atau instruktur di sekolah.

Pada pertengahan abad kesembilan belas, kemajuan mendasar terjadi di beberapa bidang. Dokter Jean Poiseuille (1799–1869) telah secara akurat mengukur aliran dalam tabung kapiler untuk berbagai macam cairan, sedangkan di Jerman Gotthilf Hagen (1797–1884) telah membedakan antara aliran laminar dan turbulen dalam pipa. Di Inggris, Lord Osborne Reynolds (1842–1912) melanjutkan penelitian tersebut (Gbr. 1–11) dan mengembangkan bilangan tak berdimensi yang menyandang namanya. Demikian pula, sejajar dengan karya awal Navier, George Stokes (1819–1903) menyelesaikan persamaan umum gerak fluida (dengan gesekan) yang mengambil namanya. William Froude (1810–1879) hampir sendirian mengembangkan prosedur dan membuktikan nilai pengujian model fisik. Keahlian Amerika telah setara dengan orang Eropa seperti yang ditunjukkan oleh karya perintis James Francis (1815–1892) dan Lester Pelton (1829–1908) di bidang turbin dan penemuan meter Venturi oleh Clemens Herschel (1842–1930).

Selain Reynolds dan Stokes, banyak kontribusi penting yang diberikan pada teori fluida pada akhir abad kesembilan belas oleh ilmuwan Irlandia dan Inggris, termasuk William Thomson, Lord Kelvin (1824–1907), William Strutt, Lord Rayleigh (1842–1919), dan Tuan Horace Lamb (1849–1934). Individu-individu ini menyelidiki sejumlah besar masalah, termasuk analisis dimensi, aliran irrotasional, gerakan pusaran, kavitasi, dan gelombang. Dalam arti yang lebih luas, karya mereka juga mengeksplorasi hubungan antara mekanika fluida, termodinamika, dan perpindahan panas.

Permulaan abad ke-20 membawa dua perkembangan besar. Pertama, pada tahun 1903, Wright bersaudara yang otodidak (Wilbur, 1867–1912; Orville, 1871–1948) menemukan pesawat terbang melalui penerapan teori dan eksperimen yang menentukan. Penemuan primitif mereka lengkap dan mencakup semua aspek utama pesawat modern (Gbr. 1–12). Persamaan Navier-Stokes sampai saat ini tidak banyak berguna karena terlalu sulit untuk diselesaikan. Dalam makalah perintisnya pada tahun 1904, Ludwig Prandtl dari Jerman (1875–1953) menunjukkan bahwa aliran fluida dapat dibagi menjadi lapisan dekat dinding, lapisan batas, yang efek gesekannya signifikan, dan lapisan luar yang efek gesekannya dapat diabaikan. dan persamaan Euler dan Bernoulli yang disederhanakan dapat diterapkan. Muridnya, Theodor von Kármán (1881–1963), Paul Blasius (1883–1970), Johann Nikuradse (1894–1979), dan lainnya, membangun teori tersebut dalam aplikasi hidrolik dan aerodinamis. (Selama Perang Dunia II, kedua belah pihak mendapat manfaat dari teori tersebut karena Prandtl tetap tinggal di Jerman sementara murid terbaiknya, von Kármán kelahiran Hongaria, bekerja di Amerika.)

Pertengahan abad ke-20 dapat dianggap sebagai masa keemasan penerapan mekanika fluida. Teori-teori yang ada cukup untuk tugas-tugas yang ada, dan sifat-sifat serta parameter fluida telah didefinisikan dengan baik. Hal ini mendukung perluasan besar-besaran pada sektor penerbangan, kimia, industri, dan sumber daya air; masing-masing mendorong mekanika fluida ke arah yang baru. Penelitian dan pekerjaan mekanika fluida pada akhir abad kedua puluh didominasi oleh perkembangan komputer digital di Amerika. Kemampuan untuk memecahkan masalah besar yang kompleks, seperti pemodelan iklim global atau optimalisasi bilah turbin, telah memberikan manfaat bagi masyarakat kita yang tidak pernah dibayangkan oleh para pengembang mekanika fluida abad kedelapan belas (Gbr. 1–13). Prinsip-prinsip yang disajikan pada halaman berikut telah diterapkan pada aliran yang berkisar dari momen pada skala mikroskopis hingga simulasi 50 tahun untuk seluruh wilayah sungai. Ini benar-benar mencengangkan.

Ke mana arah mekanika fluida pada abad kedua puluh satu dan seterusnya? Sejujurnya, bahkan ekstrapolasi terbatas di luar masa kini adalah kebodohan belaka. Namun, jika sejarah memberi tahu kita sesuatu, maka para insinyur akan menerapkan apa yang mereka ketahui untuk memberi manfaat bagi masyarakat, meneliti apa yang tidak mereka ketahui, dan bersenang-senang dalam prosesnya.

----------------------------------------------------------------------------------------------------

KINEMATIKA FLUIDA

TUJUAN

Ketika Anda selesai membaca bab ini, Anda seharusnya bisa

■ Memahami peran turunan material dalam mentransformasikan deskripsi Lagrangian dan Euler

■ Membedakan berbagai jenis visualisasi aliran dan metode menggambar karakteristik aliran fluida

■ Mengamati berbagai cara fluida bergerak dan berubah bentuk

■ Membedakan daerah aliran rotasi dan irrotasional berdasarkan sifat vortisitas aliran

■ Memahami kegunaan teorema transpor Reynolds

Kinematika fluida berkaitan dengan penggambaran gerak fluida tanpa harus mempertimbangkan gaya dan momen yang menyebabkan gerak tersebut. Dalam bab ini, kami memperkenalkan beberapa konsep kinematik yang berkaitan dengan fluida yang mengalir. Kita membahas turunan material dan perannya dalam mengubah persamaan kekekalan dari deskripsi aliran fluida Lagrangian (mengikuti partikel fluida) ke deskripsi aliran fluida Eulerian (berkaitan dengan medan aliran). Kami kemudian membahas berbagai cara untuk memvisualisasikan bidang aliran—garis arus, garis coretan, garis jalur, garis waktu, metode optik schlieren dan shadowgraph, dan metode permukaan; dan kami menjelaskan tiga cara untuk memplot data aliran—plot profil, plot vektor, dan plot kontur. Kami menjelaskan empat sifat kinematik dasar gerak dan deformasi fluida—laju translasi, laju rotasi, laju regangan linier, dan laju regangan geser. Konsep vortisitas, rotasionalitas, dan irrotasionalitas dalam aliran fluida kemudian dibahas. Terakhir, kita membahas teorema transpor Reynolds (RTT), yang menekankan perannya dalam mengubah persamaan gerak dari persamaan gerak yang mengikuti suatu sistem menjadi persamaan gerak yang berkaitan dengan aliran fluida masuk dan keluar dari volume kendali. Analogi antara turunan material untuk elemen fluida yang sangat kecil dan RTT untuk volume kendali berhingga telah dijelaskan.

Citra satelit dari badai di dekat pantai Florida; tetesan air bergerak bersama udara, memungkinkan kita memvisualisasikan gerakan berputar berlawanan arah jarum jam. Namun, sebagian besar badai sebenarnya bersifat irrotasional, sedangkan hanya intinya (mata badai) yang bersifat rotasi. StockTrek Getty RF

LAGRANGIAN DAN EULERIAN

DESKRIPSI LAGRANGIAN DAN EULERIAN

Subjek yang disebut kinematika berkaitan dengan studi tentang gerak. Dalam dinamika fluida, kinematika fluida adalah ilmu yang mempelajari bagaimana fluida mengalir dan bagaimana menggambarkan gerak fluida. Dari sudut pandang fundamental, ada dua cara berbeda untuk mendeskripsikan gerak. Metode pertama dan paling familiar adalah metode yang Anda pelajari di fisika SMA—mengikuti jalur objek individual.

Misalnya, kita semua pernah melihat eksperimen fisika di mana sebuah bola di meja biliar atau keping di meja hoki udara bertabrakan dengan bola atau keping lain atau dengan dinding (Gbr. 4–1).

Dengan sejumlah kecil benda, seperti bola bilyar di meja biliar,

objek individu dapat dilacak.

Hukum Newton digunakan untuk menggambarkan gerak suatu benda, dan kita dapat memprediksi secara akurat ke mana benda itu pergi dan bagaimana momentum dan energi kinetik berpindah dari satu benda ke benda lainnya. Kinematika eksperimen tersebut melibatkan pencatatan vektor posisi setiap benda,dan vektor kecepatan setiap benda, sebagai fungsi waktu (Gbr. 4–2).

Dalam deskripsi Lagrangian, kita harus melacak posisi dan kecepatan masing-masing partikel.

Ketika metode ini diterapkan pada fluida yang mengalir, kami menyebutnya deskripsi Lagrangian tentang gerak fluida yang diambil dari nama ahli matematika Italia Joseph Louis Lagrange (1736–1813). Analisis Lagrangian analog dengan analisis sistem (tertutup) yang Anda pelajari dalam termodinamika; yaitu, kita mengikuti sekumpulan identitas yang tetap. Deskripsi Lagrangian mengharuskan kita untuk melacak posisi dan kecepatan masing-masing bidang fluida, yang kita sebut sebagai partikel fluida, dan menganggapnya sebagai bidang dengan identitas tetap.

Seperti yang dapat Anda bayangkan, metode mendeskripsikan gerak ini jauh lebih sulit untuk zat cair dibandingkan untuk bola bilyar! Pertama-tama kita tidak dapat dengan mudah mendefinisikan dan mengidentifikasi partikel fluida saat mereka bergerak. Kedua, fluida merupakan sebuah kontinum (dari sudut pandang makroskopis), sehingga interaksi antar partikel fluida tidak mudah dijelaskan seperti interaksi antara objek berbeda seperti bola bilyar atau keping hoki udara. Selain itu, partikel fluida terus berubah bentuk ketika bergerak dalam aliran.

Dari sudut pandang mikroskopis, suatu cairan terdiri dari milyaran

molekul yang terus-menerus saling bertabrakan, seperti bola bilyar; namun tugas untuk mengikuti bahkan sebagian dari molekul-molekul ini cukup sulit, bahkan untuk komputer kita yang tercepat dan terbesar sekalipun. Namun demikian, ada banyak aplikasi praktis dari deskripsi Lagrangian, seperti pelacakan skalar pasif dalam aliran untuk memodelkan transportasi kontaminan, perhitungan dinamika gas yang dijernihkan mengenai masuknya kembali pesawat ruang angkasa ke atmosfer bumi, dan pengembangan sistem visualisasi dan pengukuran aliran. berdasarkan pelacakan partikel (seperti yang dibahas dalam Bagian 4–2).

Metode yang lebih umum untuk mendeskripsikan aliran fluida adalah deskripsi Eulerian tentang gerak fluida, yang diambil dari nama ahli matematika Swiss Leonhard Euler (1707–1783). Dalam deskripsi aliran fluida Euler, volume terbatas yang disebut domain aliran atau volume kontrol didefinisikan, yang melaluinya fluida mengalir masuk dan keluar. Daripada melacak partikel fluida individual, kami mendefinisikan variabel medan, fungsi ruang dan waktu, dalam volume kendali.

Variabel medan pada lokasi tertentu pada waktu tertentu adalah nilai variabel partikel fluida mana pun yang menempati lokasi tersebut pada waktu itu. Misalnya, medan tekanan adalah variabel medan skalar; untuk aliran fluida tiga dimensi tidak tunak secara umum dalam koordinat Kartesius,

Demikian pula medan percepatan juga merupakan variabel medan vektor,

Secara kolektif, variabel bidang ini (dan lainnya) menentukan bidang aliran. Bidang kecepatan Persamaan. 4–2 diperluas dalam koordinat Kartesius (x, y, z), (i→, j→, k→) sebagai

Ekspansi serupa dapat dilakukan untuk bidang percepatan Persamaan. 4–3. Dalam deskripsi Euler, semua variabel bidang tersebut didefinisikan di setiap lokasi (x, y, z) dalam volume kontrol dan kapan saja dalam waktu t (Gbr. 4–3).

(a) Dalam deskripsi Euler, kita mendefinisikan variabel medan, seperti medan tekanan dan medan kecepatan, di setiap lokasi dan waktu sesaat.
(b) Misalnya, alat pengukur kecepatan udara yang dipasang di bawah sayap pesawat terbang mengukur kecepatan udara di lokasi tersebut. (Bawah)
Foto oleh John M. Cimbala.

Dalam deskripsi Euler kita tidak terlalu peduli dengan apa yang terjadi pada masing-masing partikel fluida; melainkan kita memperhatikan tekanan, kecepatan, percepatan, dan lain-lain, partikel fluida mana pun yang kebetulan berada di lokasi yang diinginkan pada saat yang diinginkan.

Perbedaan kedua gambaran ini menjadi lebih jelas dengan membayangkan seseorang berdiri di tepi sungai, mengukur sifat-sifatnya. Dalam pendekatan Lagrangian, dia melemparkan sebuah wahana yang bergerak ke hilir bersama air. Dalam pendekatan Eulerian, ia menambatkan wahana tersebut pada lokasi tetap di dalam air.

Meskipun deskripsi Lagrangian sering berguna, deskripsi Euler seringkali lebih sesuai untuk aplikasi mekanika fluida. Selain itu, pengukuran eksperimental umumnya lebih sesuai dengan deskripsi Euler. Dalam terowongan angin, misalnya, probe kecepatan atau tekanan biasanya ditempatkan pada lokasi tetap dalam aliran, berukuran V→(x, y, z, t) atau P(x, y, z, t). Namun, meskipun persamaan gerak dalam deskripsi Lagrangian yang mengikuti masing-masing partikel fluida sudah diketahui dengan baik (misalnya, hukum kedua Newton), persamaan gerak aliran fluida tidak begitu mudah terlihat dalam deskripsi Euler dan harus diturunkan dengan cermat. Kami melakukan ini untuk analisis volume kendali (integral) melalui teorema transpor Reynolds di akhir bab ini. Kami memperoleh persamaan diferensial gerak di Bab. 9.

CONTOH 4–1

Bidang Kecepatan Dua Dimensi yang Stabil

Medan kecepatan dua dimensi yang stabil dan tidak dapat dimampatkan diberikan oleh

dimana koordinat x dan y dalam satuan meter dan besar dari kecepatan dalam m/s. Titik stagnasi didefinisikan sebagai titik pada medan aliran yang kecepatannya nol.

(a) Tentukan apakah terdapat titik stagnasi pada medan aliran ini dan, jika ya, di manakah?

(b) Buat sketsa vektor kecepatan di beberapa lokasi dalam domain antara x = - 2 m sampai 2 m dan

y = 0 m sampai 5 m; secara kualitatif menggambarkan bidang aliran.

Jawaban

Untuk medan kecepatan tertentu, lokasi titik stagnasi harus ditentukan. Beberapa vektor kecepatan harus dibuat sketsa dan bidang kecepatan harus dijelaskan.

Asumsi

1. Alirannya stabil dan tidak dapat dimampatkan.

2. Alirannya bersifat dua dimensi, yang berarti tidak ada komponen kecepatan z dan tidak ada variasi u atau v dengan z.

Analisis

(a) Karena V→ adalah sebuah vektor, semua komponennya harus sama dengan nol agar V→ itu sendiri menjadi nol. Menggunakan Persamaan. 4–4 dan mengatur Persamaan. 1 sama dengan nol,

Titik stagnasi:

Ya. Terdapat satu titik stagnasi yang terletak di x = - 20,625 m, y = 1,875 m.

(b) Komponen kecepatan x dan y dihitung dari Persamaan. 1 untuk beberapa lokasi (x, y) dalam rentang yang ditentukan. Misalnya, di titik (x = 2 m, y = 3 m), u = 2,10 m/s dan v = 20,900 m/s. Besarnya kecepatan (kecepatan) pada titik tersebut adalah 2,28 m/s. Di lokasi ini dan di lokasi lainnya, vektor kecepatan dibangun dari dua komponennya, yang hasilnya ditunjukkan pada Gambar 4–4.

Vektor kecepatan (panah biru) untuk bidang kecepatan Contoh 4–1. Skala ditunjukkan oleh panah atas, dan kurva hitam pekat mewakili perkiraan bentuk beberapa garis arus, berdasarkan vektor kecepatan yang dihitung. Titik stagnasi ditunjukkan dengan lingkaran biru. Daerah yang diarsir mewakili sebagian bidang aliran yang dapat memperkirakan aliran ke saluran masuk (Gbr. 4–5).

Bidang aliran di dekat saluran masuk mulut lonceng bendungan pembangkit listrik tenaga air; sebagian dari medan kecepatan pada Contoh soal 4–1 dapat digunakan sebagai perkiraan orde pertama dari medan aliran fisik ini. Daerah yang diarsir sesuai dengan Gambar 4-4.

Aliran tersebut dapat digambarkan sebagai aliran titik stagnasi dimana aliran masuk dari atas dan bawah dan menyebar ke kanan dan kiri terhadap suatu simetri lipat horizontal pada y = 1,875 m. Titik stagnasi bagian (a) ditunjukkan dengan lingkaran biru pada Gambar 4–4. Jika kita hanya melihat bagian yang diarsir pada Gambar 4-4, bidang aliran ini memodelkan aliran yang konvergen dan dipercepat dari kiri ke kanan. Aliran seperti itu mungkin ditemui, misalnya, di dekat saluran masuk mulut lonceng bendungan pembangkit listrik tenaga air (Gbr. 4–5). Bagian yang berguna dari medan kecepatan yang diberikan dapat dianggap sebagai perkiraan orde pertama dari bagian yang diarsir dari medan aliran fisik pada Gambar 4-5.

Bidang Akselerasi ( Acceleration Field )

Seperti yang harus Anda ingat dari studi Anda tentang termodinamika, hukum kekekalan dasar (seperti kekekalan massa dan hukum pertama termodinamika) dinyatakan untuk sistem identitas tetap (disebut juga sistem tertutup). Dalam kasus di mana analisis volume kendali (juga disebut sistem terbuka) lebih mudah dilakukan dibandingkan analisis sistem, hukum dasar ini perlu ditulis ulang ke dalam bentuk yang dapat diterapkan pada volume kendali.

Prinsip yang sama berlaku di sini. Faktanya, terdapat analogi langsung antara sistem versus volume kendali dalam termodinamika dan deskripsi Lagrangian versus Euler dalam dinamika fluida. Persamaan gerak aliran fluida (seperti hukum kedua Newton) ditulis untuk partikel fluida, yang disebut juga partikel material. Jika kita mengikuti partikel fluida tertentu ketika bergerak dalam aliran, kita akan menggunakan deskripsi Lagrangian, dan persamaan gerak akan dapat diterapkan secara langsung.

Misalnya, kita akan mendefinisikan lokasi partikel di ruang angkasa dalam bentuk vektor posisi material

Namun, beberapa manipulasi matematis kemudian diperlukan untuk mengubah persamaan gerak menjadi bentuk yang dapat diterapkan pada deskripsi Euler.

Misalnya, hukum kedua Newton yang diterapkan pada partikel fluida kita,

dimana adalah gaya total yang bekerja pada partikel fluida, adalah massanya, dan adalah percepatannya (Gbr. 4–6). Menurut definisinya,

percepatan partikel fluida adalah turunan waktu dari kecepatan partikel,

Namun, pada saat tertentu dalam waktu t, kecepatan partikel sama dengan nilai lokal medan kecepatan di lokasi partikel , karena partikel fluida bergerak bersama fluida menurut definisinya. Dengan kata lain,

Untuk mengambil turunan waktu dalam Persamaan. 4–6, oleh karena itu kita harus menggunakan aturan rantai, karena variabel terikat ( $\overrightarrow{V}$ ) merupakan fungsi dari empat variabel bebas $X_{partikel},Y_{pertikel},Z_{partikel}$ dan t .